Така е Валери, Иванов не е казал защо.

Дотук бяхме с 4-ти клас. Нататък става по-сложно (не е за всеки, както е писал Петър Берон в букваря)
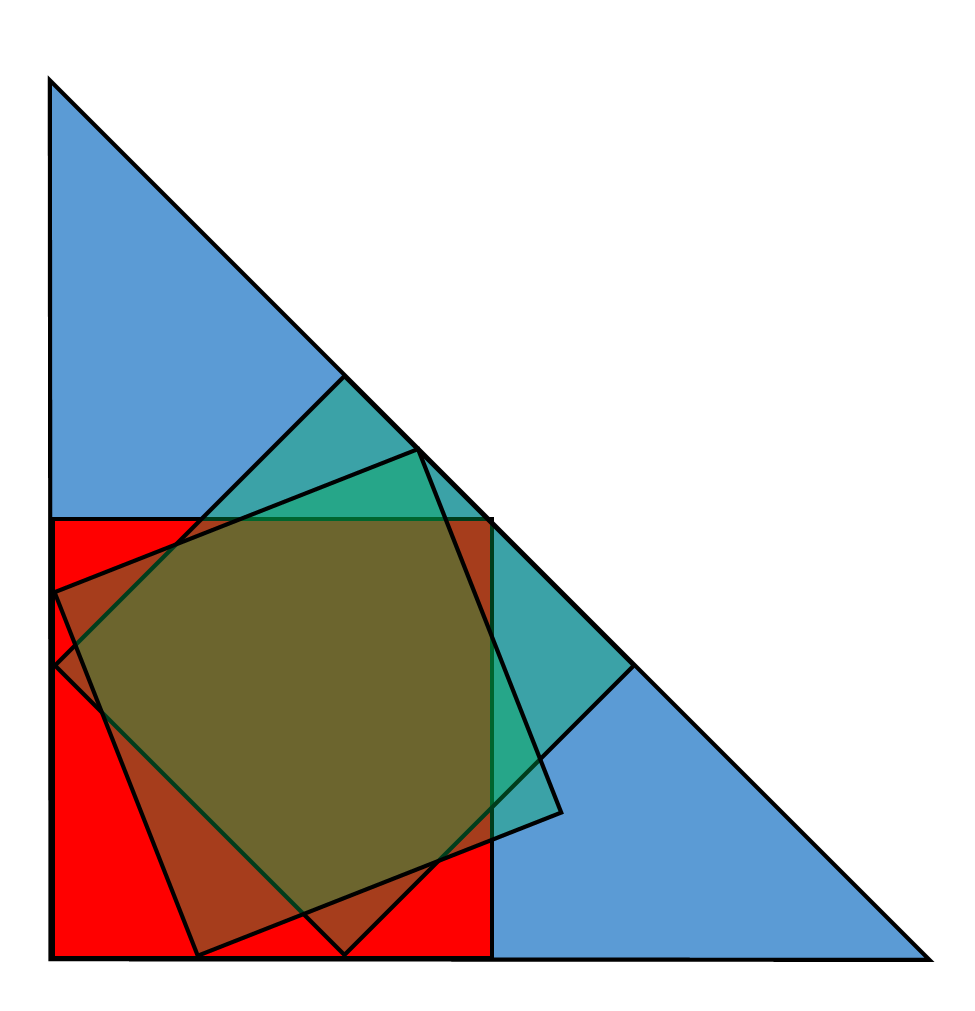
На долната картинка съм показал 3 положения на квадрата. Двете дотук описани и едно случайно между тях (със само 3 върха вписани в триъгълника).
Вижда се че площта на този трети квадрат е най-малка.
Това означава, че от всички възможни вписани квадрати,
дефинирани чрез ъгъла на завъртане спрямо долната страна на триъгълника,
(тоест за червения квадрат ъгълът на завъртане е нула),
някъде има минимум (или повече минимуми, но поне един).
Да се намери при какъв ъгъл на завъртане имаме най-малък квадрат. Може и числено, но в идеалния случай - алгебрично.
2024-11-17_16-41-39-844.png (30.46 KиБ) Видяна 2140 пъти
Дотук бяхме с 4-ти клас. Нататък става по-сложно (не е за всеки, както е писал Петър Берон в букваря)
На долната картинка съм показал 3 положения на квадрата. Двете дотук описани и едно случайно между тях (със само 3 върха вписани в триъгълника).
Вижда се че площта на този трети квадрат е най-малка.
Това означава, че от всички възможни вписани квадрати,
дефинирани чрез ъгъла на завъртане спрямо долната страна на триъгълника,
(тоест за червения квадрат ъгълът на завъртане е нула),
някъде има минимум (или повече минимуми, но поне един).
Да се намери при какъв ъгъл на завъртане имаме най-малък квадрат. Може и числено, но в идеалния случай - алгебрично.
Прикачен файл:
2024-11-17_16-41-39-844.png (30.46 KиБ) Видяна 2140 пъти
Последна промяна от Lisko на пет яну 03, 2025 8:36 am, променено общо 2 пъти.
